Macam-Macam Bangun Ruang dan Gambarnya - Dalam pelajaran matematika, kita pasti akan menjumpai pembahasan mengenai bangun datar dan bangun ruang. Bangun datar merupakan bangun dua dimensi, sedangkan bangun ruang merupakan bangun tiga dimensi. Nah, pada kesempatan kali ini kita akan mempelajari macam-macam bangun ruang lengkap dengan rumus dan gambarnya.
Sebelum membahas mengenai macam-macam bangun ruang, sebaiknya kita memahami terlebih dahulu apa itu bangun ruang. Sehingga nantinya kita akan lebih mudah dalam memahami dan membedakannya antara bangun ruang yang satu dengan lainnya. Berikut adalah sedikit penjelasan mengenai pengertian bangun ruang.

Bangun ruang adalah bangun tiga dimensi yang mempunyai volume atau isi. Disebut sebagai bangun tiga dimensi karena mempunyai tiga unsur penyusunnya, yakni rusu, titik sudut dan bidang sisi permukaan.
Rusuk pada bangun ruang merupakan ruas garis yang mempertemukan dua sisi permukaan bangun ruang. Sedangkan titik sudut merupakan titik hasil pertemuan antara rusuk-rusuknya. Sementara bidang sisi adalah luas bidang yang membentuk bangun ruang.
Dalam keseharian, kita juga sering menjumpai banyak sekali contoh bangun ruang yang ada di sekeliling kita. Misalnya saja rubrik yang berbentuk kubus, cokelat batang yang berbentuk prisma, kaleng susu yang berbentuk tabung, es krim yang berbentuk kerucut dan berbagai macam jenis bola yang merupakan bnetuk dari bangun ruang bola.
Setiap bangun ruang tentu mempunyai karakteristik yang berbeda antara yang satu dengan yang lainnya. Perbedaan tersebut didasari oleh jumlah rusuk, jumlah titik sudut, dan bentuk bidang sisi permukaannya. Perbedaan itu yang nantinya menjadi dasar dalam penamaan nama macam-macam bangun ruang.
Macam-Macam Bangun Ruang
Bangun ruang terdiri dari kubus, balok, kerucut, limas, prisma, tabung dan bola. Berikut adalah pembahasan masing-masing bangun ruang yang meliputi pengertian, sifat, rumus dan gambarnya.
1. Kubus
Kubus adalah bangun ruang tiga dimensi yang mempunyai panjang rusuk yang sama. Kubus dibentuk oleh enam sisi yang berukuran sama besar, yaitu sisi-sisi berbentuk persegi. Contoh benda berbentuk bangun ruang kubus adalah rubik dan dadu. Berikut merupakan contoh gambar bangun ruang kubus.

Berikut sifat-sifat yang dimiliki oleh bangun ruang kubus:
- Memiliki 6 buah sisi permukaan
- Memiliki 12 rusuk
- Memiliki 8 buah titik sudut
- Memiliki 12 diagonal bidang
- Memiliki 4 diagonal ruang
- Memiliki 6 bidang diagonal
- Sisi-sisi kubus berbentuk persegi
- Rusuk kubus sama panjang
- Diagonal bidang berukuran sama panjang
- Panjang diagonal ruang memiliki ukuran yang sama
- Masing-masing bidang diagonal pada kubus berbentuk persegi panjang
Berikut rumus yang digunakan untuk menghitung luas dan volume bangun ruang kubus:
- Rumus luas permukaan kubus = 6 x sisi x sisi
- Rumus volume kubus = sisi x sisi x sisi
2. Balok
Balok adalah bangun tiga dimensi yang terbentuk oleh tiga pasang sisi berbentuk segi empat. Sisi-sisi yang saling berhadapan mempunyai ukuran yang sama besar. Contoh benda yang mempunyai bentuk balok antara lain kulkas, lemari baju dan kotak pensil. Berikut ini merupakan contoh gambar bangun ruang balok.
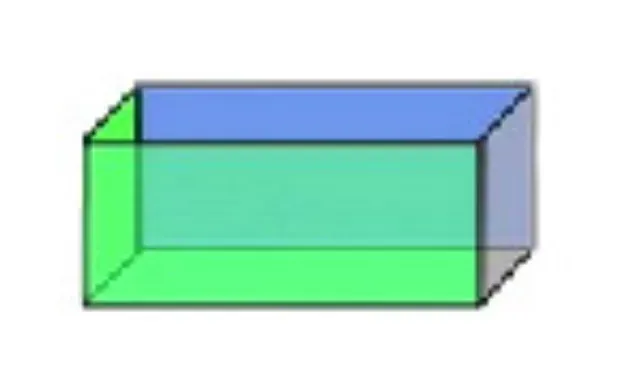
Berikut ini adalah sifat-sifat yang dimiliki oleh bangun ruang balok:
- Memiliki 6 buah bidang sisi
- Memiliki 12 rusuk, yaitu 4 rusuk panjang, 4 rusuk lebar, dan 4 rusuk tinggi
- Memiliki 8 buah titik sudut
- Memiliki 12 diagonal bidang
- Memiliki 4 diagonal ruang
- Memiliki 6 bidang diagonal
- Sisi-sisi balok berbentuk persegi dan persegi panjang
- Rusuk-rusuk balok yang sejajar berukuran sama panjang
- Panjang diagonal balok pada bidang pada sisi yang berhadapan sama panjang
- Diagonal ruang balok berukuran sama panjang
- Bidang diagonal balok berbentuk persegi panjang
Berikut adalah rumus yang digunakan untuk menghitung luas dan volume bangun ruang balok:
- Rumus luas permukaan balok = 2 × ( panjang x lebar + lebar x tinggi + panjang x tinggi)
- Rumus volume balok = panjang × lebar × tinggi
Baca juga : Unsur-Unsur Balok Beserta Gambarnya
3. Limas
Limas adalah bangun ruang tiga dimensi yang mempunyai bentuk bidang alas segi-n. Sisi tegak bangun ruang limas berbentuk segitiga yang bertemu pada satu titik yang tegak lurus dengan alas limas. Limas terdiri dari beberapa macam jenis, diantaranya adalah limas segitiga, limas segiempat, limas segilima dan limas segieman. Berikut di bawah ini adalah contoh gambar bangun ruang limas segi empat.

Berikut adalah sifat dan ciri yang dimiliki oleh limas:
- Mempunyai (n+1) buah bidang sisi
- Mempunyai (n+1) buah titik sudut
- Mempunyai 2n buah rusuk
- Tidak semua limas mempunyai diagonal bidang, diagonal ruang dan bidang diagonal
- Limas mempunyai sisi yang jumlahnya tergantung dari bentuk alasanya. Misalnya limas segi empat mempunyai lima buah sisi (satu sisi alas berbentuk segi empat dan empat sisi tegak berbentuk segitiga)
Berikut adalah rumus yang digunakan untuk menghitung luas dan volume bangun limas:
- Rumus luas permukaan limas = Luas alas + Luas sisi tegak/selubung limas
- Rumus volume limas = 1/3 × Luas alas × tinggi
Baca juga : Unsur-Unsur Limas Beserta Penjelasannya
4. Prisma
Prisma adalah bangun tiga dimensi yang dibentuk oleh bidang alas dan atap berbentuk segi-n yang kongruen. Contoh benda berbentuk bangun ruang prisma adalah tenda, atap rumah dan batang coklat. Sama seperti limas, prisma juga terdiri dari beberapa macam jenis, seperti prisma segitiga, prisma segiempat, prisma segilima, dan seterusnya. Berikut adalah contoh gambar bangun prisma segitiga.

Berikut adalah sifat dan ciri yang dimiliki oleh prisma:
- Mempunyai (n+2) buah bidang sisi
- Mempunyai 2n buah titik sudut
- Mempunyai 3n buah rusuk
- Mempunyai n(n–1) buah diagonal sisi
- Mempunyai n(n–3) diagonal ruang
- Mempunyai ½ n(n–1) bidang diagonal jika n genap
- Mempunyai ½ n(n–3) bidang diagonal jika n ganjil
- Alas dan atap prisma mempunyai bentuk yang kongruen (sebangun/sama)
- Sisi-sisi samping prisma berbentuk persegi panjang
- Diagonal bidang pada sisi yang sama, mempunyai ukuran sama panjang
- Prisma mempunyai rusuk yang tegak, tetapi ada juga yang tidak tegak
Berikut adalah rumus yang digunakan untuk menghitung luas dan volume bangun prisma:
- Rumus luas permukaan prisma = (2 × Luas alas) + (Keliling alas × tinggi)
- Rumus volume prisma = Luas alas × tinggi
Baca juga : Unsur-Unsur Prisma Beserta Pembahasannya
5. Kerucut
Kerucut adalah bangun ruang tiga dimensi yang dibentuk oleh alas berbentuk lingkaran dan sisi selimut yang berbentuk juring lingkaran. Kerucut memiliki satu buah titik sudut dan satu rusuk. Sedangkan jumlah bidang sisinya ada dua, yakni sisi lingkaran pada bagian alas dan sisi samping yang menyelimuti keliling lingkaran hingga titik sudutnya. Berikut adalah contoh gambar kerucut.

Berikut adalah ciri-ciri dan sifat bangun ruang kerucut:
- Memiliki dua bidang sisi (alas berbentuk lingkaran dan sisi selimut berbentuk juring lingkaran)
- Memiliki satu buah rusuk berbentuk lengkung
- Memiliki satu buah titik sudut sebagai titik puncak
Berikut adalah rumus yang digunakan untuk menghitung luas dan volume bangun kerucut:
- Rumus luas permukaan kerucut = ( π × r² ) + ( π × r × s)
- Rumus volume kerucut = 1/3 × π × r² × t
Keterangan:
π = 22/7 atau 3,14
r = jari-jari kerucut
s = garis pelukis kerucut
t = tinggi kerucut
Baca juga : Unsur-Unsur Kerucut Beserta Gambar dan Pembahasannya
6. Tabung
Tabung adalah bangun ruang tiga dimensi yang mempunyai sisi alas dan sisi atas (tutup) berbentuk lingkaran, serta bidang sisi tegak tabung membentuk lengkungan yang disebut dengan selimut tabung. Jarak antara sisi alas dengan sisi atas merupakan tinggi tabung. Berikut di bawah ini adalah contoh gambar bangun ruang tabung.
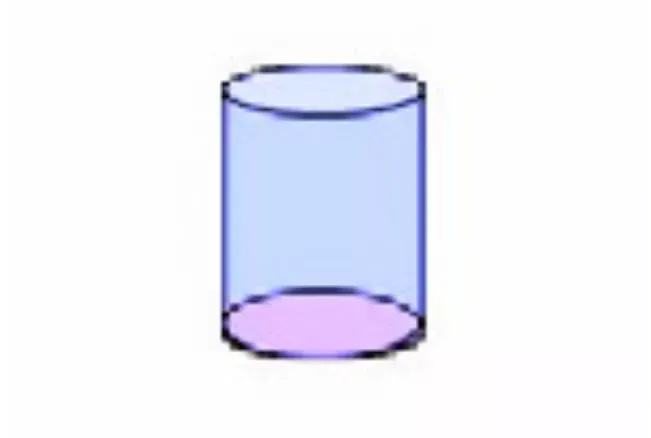
Berikut adalah sifat-sifat dan ciri yang dimiliki oleh bangun tabung:
- Memiliki 3 buah sisi (dua buah sisi berbentuk lingkaran dan satu sisi selimut berbentuk persegi panjang)
- Memiliki 2 buah rusuk lengkung
- Memiliki alas dan atap/tutup berbentuk lingkaran
- Tidak memiliki titik sudut
Berikut adalah rumus-rumus yang digunakan untuk menghitung luas dan volume bangun tabung:
- Rumus luas permukaan tabung = (2 × Luas alas) + (Keliling alas × tinggi tabung)
- Rumus volume tabung = π × r² × t
Keterangan
π = 22/7 atau 3,14
r = jari-jari tabung
t = tinggi tabung
Baca juga : Unsur-Unsur Tabung Beserta Rumus dan Gambarnya
7. Bola
Bola merupakan bangun ruang tiga dimensi yang mempunyai bidang sisi permukaan berbentuk lengkung. Bidang sisi pada bola mempunyai jarak yang sama pada sebuah titik pusat. Bangun ruang bola merupakan bagun ruang yang tidak memiliki rusuk. Bola adalah bangun ruang yang dibatasi oleh satu bidang sisi lengkung. Berikut di bawah ini adalah contoh gambar bentuk bangun ruang bola:
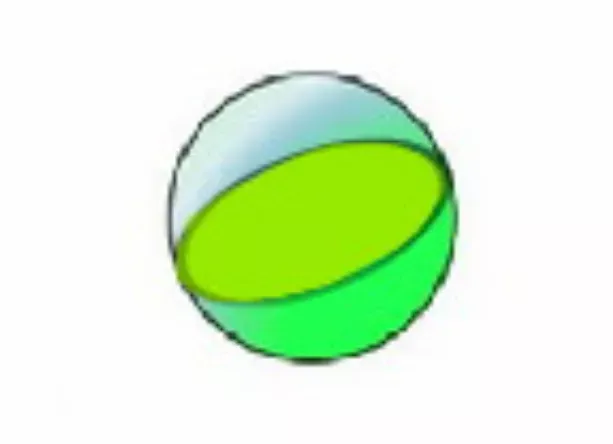
- Memiliki satu buah bidang sisi berbentuk lengkung
- Memiliki satu buah titik pusat
- Tidak memiliki titik sudut
- Tidak memiliki rusuk
- Memiliki jari jari yang sama panjang dan tak terhingga
Berikut adalah rumus-rumus yang dapat digunakan untuk menghitung luas dan volume bangun bola:
- Rumus luas permukaan bola = 4 × π × r²
- Rumus volume bola = 4/3 × π × r3
Keterangan
π = 22/7 atau 3,14
r = jari-jari bola
Baca juga : Unsur-Unsur Bola Beserta Rumus dan Pembahasannya
Demikianlah penjelasan mengenai macam bangun ruang beserta sifat, rumus dan gambarnya. Semoga tulisan di atas dapat bermanfaat bagi para pembaca. Terimakasih.