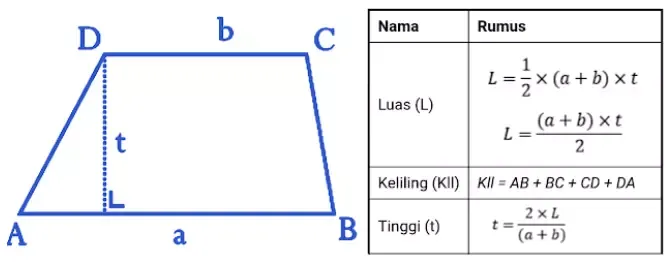
Pada kesempatan ini, kita akan mengulas secara menyeluruh mengenai rumus-rumus trapesium, termasuk rumus untuk luas dan kelilingnya. Apakah Anda sudah familiar dengan cara menghitung luas dan keliling sebuah trapesium? Jika belum, mari kita lihat pembahasannya di bawah ini.
Trapesium adalah bangun datar segi empat yang memiliki dua sisi yang sejajar dan tidak sama panjang. Selain itu, trapesium juga memiliki dua sisi lain yang tidak sejajar dan tidak sama panjang. Terdapat tiga jenis trapesium, yaitu trapesium siku-siku, trapesium sama kaki, dan trapesium sembarang.
Seperti halnya bangun datar lainnya, trapesium memiliki ciri khas tersendiri yang mempermudah dalam mengenali bentuknya. Berikut adalah beberapa ciri khas dari trapesium yang perlu diketahui.
- Memiliki empat sisi
- Memiliki dua sisi yang sejajar, namun tidak sama panjang
- Memiliki empat sudut
- Total sudut yang berjejer adalah 180°
- Jumlah total sudutnya adalah 360°
- Memiliki luas, dengan rumus luas trapesium adalah ½ × (AB + CD) × tinggi
- Memiliki keliling, dengan rumus keliling trapesium adalah AB + BC + CD + DA
Berikut ini adalah rumus matematika yang digunakan untuk menghitung luas, keliling, dan tinggi trapesium.
Rumus Trapesium
1. Luas Trapesium
Sebagai bangun datar, trapesium memiliki luas dan keliling yang dapat dihitung menggunakan rumus matematika. Meskipun terbagi menjadi beberapa jenis, namun rumus untuk mencari luas trapesium tetap sama, yaitu 1/2 dikali jumlah sisi sejajar dikali tinggi.
| L = 1/2 (a + b) x t |
Keterangan:
L = luas trapesium
a, b = sisi sejajar trapesium
t = tinggi trapesium
2. Keliling Trapesium
Keliling trapesium adalah jumlah total panjang semua sisinya pada bangun datar trapesium. Berikut adalah rumus yang bisa digunakan untuk menghitung keliling trapesium.
| K = S1 + S2 + S3 + S4. |
Keterangan:
K = keliling trapesium
s = sisi trapesium
3. Tinggi Trapesium
Selain menghitung keliling dan luasnya, kita juga harus bisa menghitung tinggi dan sisi-sisi trapesium. Untuk mencari tinggi trapesium, kita dapat menggunakan rumus berikut.
| t = (2 x L) : (a + b) |
| a = [(2 x L) : t ] – b |
| b = [(2 x L) : t ] – a |
Keterangan:
t = tinggi trapesium
L = luas trapesium
a = sisi sejajar 1
b = sisi sejajar 2
Agar bisa memahami penggunaan rumus-rumus trapesium di atas, penting untuk mencoba beberapa contoh soal tentang perhitungan trapesium. Berikut ini adalah contoh penerapan rumus trapesium dalam soal-soal tentang perhitungan trapesium.
Contoh Soal
1. Hitunglah luas dan keliling bangun trapesium pada gambar berikut ini!
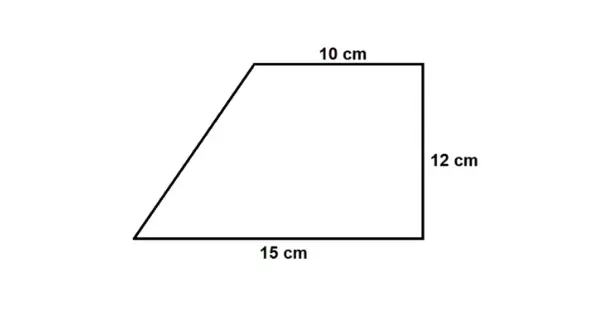
Penyelesaian:
L = 1/2 x (a + b) x t
L = 1/2 x (10+15) x 12
L = 1/2 x 25 x 12
L = 150 cm².
Sebelum menghitung keliling trapesium, terlebih dahulu kita harus mencari ukuran sisi yang belum diketahui (sisi miring).
s = √12² + (15 – 10)²
s = √12² + 5²
s = √144 + 25
s = √169
s = 13 cm.
K = s1 + s2 + s3 + s4
K = 10 + 12 + 15 + 13
K = 50 cm
Jadi, keliling trapesium adalah 50 cm.
2. Diketahui sebuah bangun trapesium memiliki luas 100 cm². Sedangkan ukuran masing-masing sisi sejajarnya adalah 12 cm dan 8 cm. Hitunglah tinggi trapesium tersebut!
Penyelesaian:
t = (2 x L) : (a + b)
t = (2 x 100) : (12 + 8)
t = 200 : 20
t = 10 cm
Jadi, tinggi trapesium adalah 10 cm.
3. Diketahui sebuah bangun trapesium memiliki luas 80 cm². Tinggi trapesium tersebut yaitu 10 cm. Sedangkan panjang salah satu sisi sejajarnya adalah 6 cm. Hitunglah berapa panjang sisi sejajar yang lainnya!
Penyelesaian:
a = [(2 x L) : t ] – b
a = [(2 x 80) : 10] – 6
a = (160 : 10) – 6
a = 16 – 6
a = 10 cm.
Demikianlah penjelasan lengkap mengenai rumus-rumus trapesium beserta contoh soal dan pembahasannya. Semoga bermanfaat.